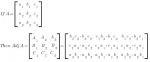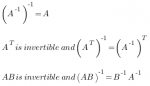Suppose the random variable distribution of a random variable X is as follows: X = xi P(x = xi) x1 x2 x3 . . . xn P1 P2 P3 . . . Pn Then, Arithmetic Mean μ = Variance σ2 […]
Arithmetic Mean, Variance and Standard Deviation of a Random Variable Distribution Read More »
MathematicsInverse of a Matrix Suppose A is a given matrix. If there exists a matrix B such that, AB = I = BI then A is said to be an invertible matrix and B is called as inverse of A
Inverse of a Matrix Read More »
MathematicsAdjoint of a Matrix If A is a square matrix then the transpose of a matrix obtained by replacing the elements of A by their co-factors is called the adjoint of a matrix A and is denoted by Adj A.
Define Adjoint of a Matrix Read More »
MathematicsA is a square matrix. If |A| = 0 , then A is called singular and if |A| ≠ 0 then A is called as a non-singular matrix. Theorems:- If A is a non-singular matrix then If A is non-singular
Singular and Non-Singular Matrix Read More »
MathematicsAccording to Multiplication Theorem of Probability, for any two events A, B probability of A∩B is as given below P(A∩B) = P(A).P(B/A) = P(B).P(A/B) Suppose N is the total number of simple events in the sample space S. Simple events
Multiplication Theorem of Probability Read More »
Mathematics