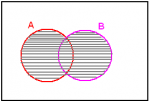
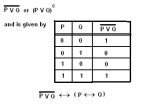
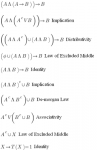Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-tabs2.php on line 433

Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-recentposts.php on line 171

Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-relatedposts.php on line 179

Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-authorposts.php on line 176

Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-popular.php on line 195

Deprecated: Function create_function() is deprecated in /home/techwond/public_html/wp-content/themes/spike/functions/widget-catposts.php on line 187
fuzzy-logic - Tech-Wonders.com

fuzzy-logic Archive

What is Fuzzy Set Theory?

What is Fuzzy Set Theory?

fuzzy-logic
Problems in the real world turn out to be quite complex, due to uncertainty in the parameters that define the problem and due to uncertainty in the situations in which that particular problem occurs. Probability theory is an age old theory, which excellently handles ...Read More
Operations on Crisp Sets 1

Operations on Crisp Sets

fuzzy-logic, Security
As you may already know, Crisp Sets consists of well-defined collection of objects. Well-defined in the sense that the objects either belong to or doesn’t belong to a set. Here are some of the most important operations of Crisp sets: Union The union of ...Read More
The Compound Proposition Exclusive NOR 2

The Compound Proposition Exclusive NOR

fuzzy-logic
The compound proposition exclusive NOR is represented as Logical Proofs :- P : a person is engineer Q : a person is mathematician R : a person is logical thinker S : a person who believes in magic Hypothesis :- Engineers are mathematicians. Logical ...Read More