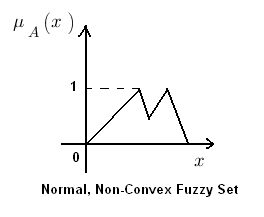Fuzzy Membership Functions and its Features

Membership Functions

Membership functions characterize the fuzzyness in a fuzzy set.

Features of Membership Functions :-

1. Core of a Membership Function :-

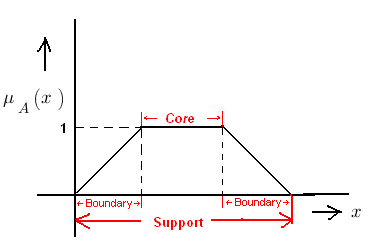
   Core of a membership function for a fuzzy set A is defined as that region of universe that is characterized by complete or full membership in the set A. Therefore core consists of all those elements X of universe of discourse, such that

   

2. Support of a Membership Function :-

   
   Support of a membership function for a fuzzy set A is defined as that region of universe that is characterized by non-zero membership in the fuzzy set A. So support consists of all those elements X of universe, such that

   

3. Boundary of a Membership Functions :-

   Boundary of a membership function for a fuzzy set A is defined as that region of universe X, that is characterized by non-zero membership but not complete membership. Boundaries comprises that part of elements X of Universe of Discourse whose membership value is given by

   

   Core, Support and Boundary of a membership function representation

   

4. Cross-over Points of a Membership Function :-

   It is defined as the elements of a fuzzy set A whose membership value is equal to 0.5

   

5. Height of a Membership Functions :-

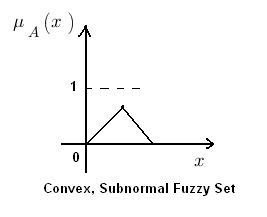
   Height of a membership function is the maximum value of the membership function. If the height of a fuzzy set is < 1 then it subnormal fuzzy set. Whereas if its height is equal to 1 then it is a normal fuzzy set.

6. Normal Fuzzy Set :-

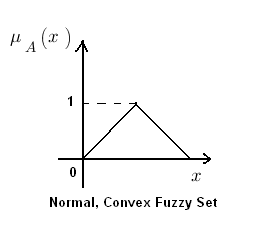
   A normal fuzzy set is one that consists of at-least one element ‘x’ of universe whose membership value is unity. For fuzzy sets where only one element which has a membership value of unity, that particular element is called prototype of the fuzzy set or prototypical element.

7. Convex Fuzzy Set :-

   Convex fuzzy set is described by a membership function whose membership values are strictly Monotonically Increasing or Monotonically Decreasing or Initially Monotonically Increasing then Monotonically Decreasing with the increase in the values of the elements of that particular fuzzy set.



  




Note: The intersection of two convex fuzzy sets is also a convex fuzzy set.



8. Fuzzy Number :-

   If ‘A’ is a convex single point normal fuzzy set defined on real line, then ‘A’ is called Fuzzy Number.

   

Fuzzification

Fuzzification is the process of making a crisp quantity fuzzy. The reverse of this process is called anti-fuzzification.