Every polynomial is not differentiable at some point, this is known to be the domain or range of that polynomial. The lower range is called the Minima and the upper range is the Maxima of the polynomial. The critical point calculator by calculator-online.net is an excellent tool to find the maxima and the minima value of the polynomial. The lower and the upper range is also known to be the lower or the upper limit of the polynomial. You may be thinking about how to find critical points of polynomials as it is one of the most essential things to learn about the range of polynomials. For simplicity, you may say the critical point is the point where you would be enabled to find the gradient of a function.
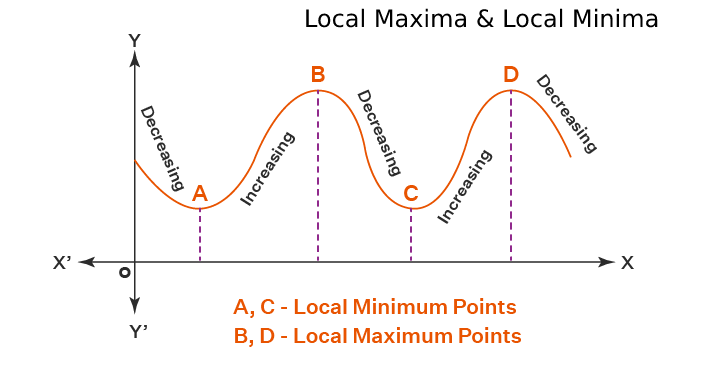
Maxima and Minima?
As you have learned that Maxima and Minima are the points, where you would not able to find the gradient. It means you would not able to find the derivative of the polynomial at the lower and the upper limit of the point. So we enter the values of the maxima and the minima in the derivative and solve the values. On the other hand, you can always get math assignment help from a real tutor who will help you to solve the values. Or you can try the critical points calculator which is a free online tool to find the maxima and minima of polynomials. The critical number calculator is easy to find the maxima and minima as you just need to enter the values of the polynomial here.

Practical Example:
Let’s consider a function 4x² + 8xy + 2y, we are using the critical point calculator to find the maxima and minima values.
Step 1:
The Derivative with Respect to “x”:
First find the derivative with respect to “x”:
F(x)=4x²+ 8xy+ 2y
Apply the power rule on the function
∂/∂x = 8x+ 8(1) y+0
∂/∂x = 8x+8y+0
∂/∂x = 8x+8y
Find the derivative with respect to “x” by the 4x²+ 8xy+ 2y by the critical point calculator.
The Derivative with Respect to “y”:
Secondly find the derivative with respect to “y”:
F(y)=4x²+ 8xy+ 2y
Use the power rules to find the derivative with respect to the “y”
y goes to the “1”
∂/∂y = 0+ 8x(1)+ 2(1)
∂/∂y = 8x(1)+ 2(1)
∂/∂y = 8x+ 2
Step 2:
Now computing the maxima and the minima, you need to compute the derivative with the Zero.
Now:
∂/∂x = 0
8x+8y=0———–(1)
∂/∂y = 0
8x+2=0———–(2)
Now to find the maxima and minima, we can use the critical point calculator.
Step 3:
Gather the values of the x from equation (2), and substitute the value in equation (1)
Let’s find the value of the “x”
8x+ 2=0
Then
x = -2/8 or x=-1/4
Input the value of the x=-1/4 in the equation (1), to find the values of the “y”
8x+8y=0———–(1)
8(-¼)+8y=0
Then
-2+8y=0
y=2/8=1/4
y =1/4
Now x=-¼ and y =¼ in the cartesian coordinate, here these values are actually the maxima and minima values of the function 4x²+ 8xy+ 2y. It is essential to find the critical point of a polynomial function just to find the maximum and the minimum range of a polynomial function.
Conclusion:
The maxima and the minima values are critical as you would not be able to find any gradient or derivative at this point. You can draw the graph of any polynomial function by finding the maxima and minima values of the polynomial function. The free online critical point calculator is a good source to find the maxima and minima values, here you just need to enter the polynomial and click the calculate button. You also learn the calculation of the maxima and minima when using the online tool.